3.3.3. Cấu kiện nén đúng tâm

Các trạng thái giới hạn của cấu kiện cứng (ngắn) chịu nén được xác định bằng sự phát triển của biến dạng dẻo khi đạt ứng suất chảy, còn của các cấu kiện mảnh (dài) – sự mất ổn định.

a. Tính về bền

Đối với những thanh ngắn (cứng), chiều dài không lớn quá 5 – 6 lần bề rộng tiết diện. Trạng thái giới hạn là khi ứng suất đạt giới hạn chảy, nên công thức tính toán cũng giống như của thanh chịu kéo

b. Tính về ổn định

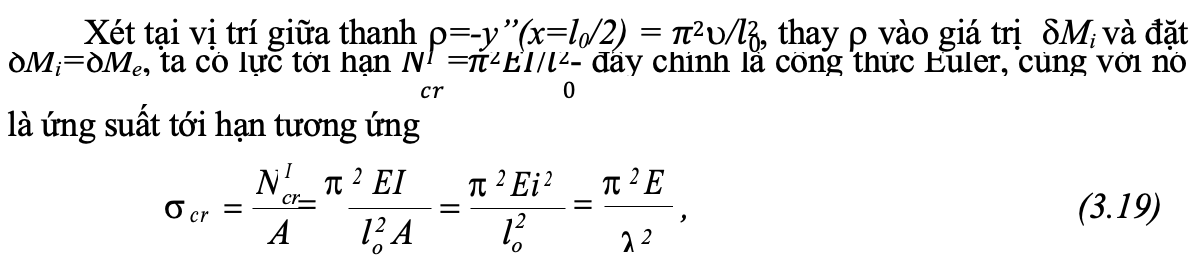
Trong đó: A - diện tích tiết diện thanh; i = Căn bậc I/A  - bán kính quán tính;   l0 i - độ mảnh; lo=l/n=l - chiều dài tính toán (khoảng cách giữa các điểm ngăn cho thanh không bị cong, xem hình 3.12); - hệ số xét điều kiện liên kết hai đầu thanh; n – số lượng nửa sóng hình sin, n là số nguyên dương, tùy theo giá trị n (n=1, 2, 3, …), sẽ ứng với các đường cong dạng thứ 1, thứ 2, thứ 3 khi mất ổn định.

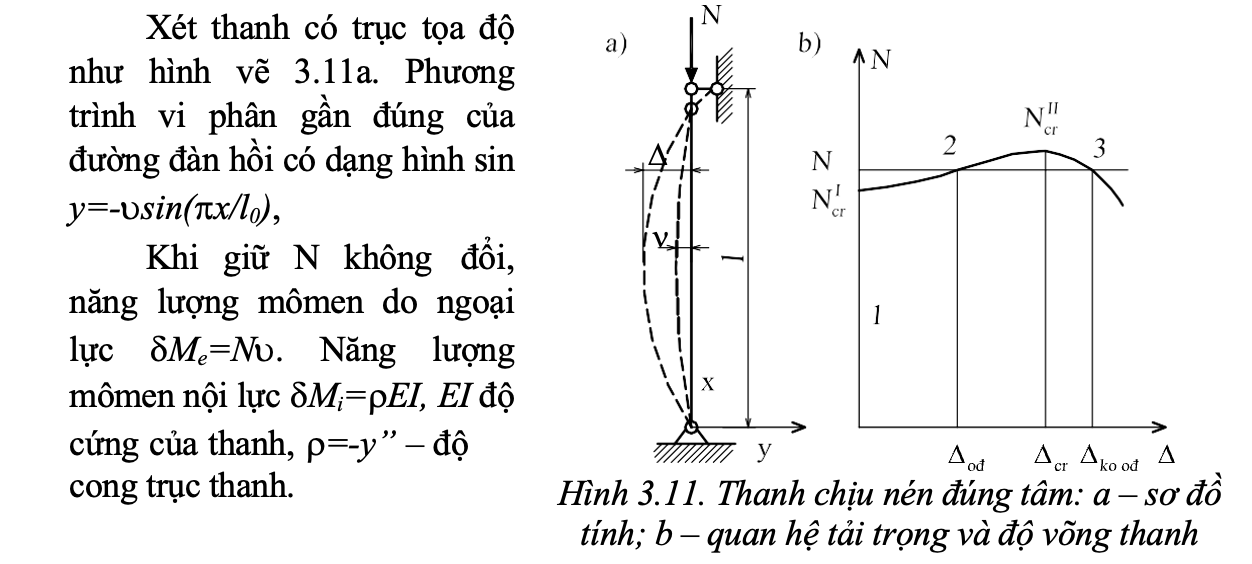
Còn có thể xem xét sự làm việc của thanh chịu nén theo độ cong trục thanh như sau:

- Khi lực nén còn nhỏ hơn lực tới hạn N  N cr thanh chịu nén ở vào trạng thái cân bằng ổn định.

- Khi lực nén đạt tới trị số tới hạn N  N cr , =0 (điểm 1, hình 3.11,b) và dN/d=0. Đường cong =(N) nằm ngang. Đây là trạng thái cân bằng phân nhánh (cân bằng thẳng và cân bằng cong).

- Khi lực nén đạt tới trị số tới hạn N  N cr , >0 thanh có thể trong trạng thái ổn định (điểm 2, hình 3.11,b) và mất ổn định (điểm 3, hình 3.11,b) với cùng một giá trị lực nén N. Thanh không còn thẳng nữa, bị uốn cong trong mặt phẳng có độ cứng nhỏ nhất ở trạng thái cân bằng cong (hình 3.11, a). Sau đó, dù tải trọng chỉ tăng rất ít, thanh cũng bị cong rất nhanh và mất khả năng chịu lực. Ứng với >0 lực tới hạn ký hiệu N II (loại II).

Thực tế thép là vật liệu đàn dẻo, khi  tăng, ứng suất đạt nhanh đến c và vùng biến hình dẻo ăn sâu vào tiết diện; tiết diện bị giảm yếu không chịu nổi tải trọng nữa. Do đó, thanh mất khả năng chịu lực gần như đồng thời với mất ổn định loại 1- NI . Ta có thể coi lực tới hạn Euler là giới hạn khả năng chịu lực của thanh nén đúng tâm. Biểu đồ thực tế N- của thanh đàn dẻo không giống như biểu đồ lý thuyết của thanh đàn hồi nói trên: sau khi đạt Ncr, thanh có biến dạng đàn hồi, lực N tăng được một chút rồi giảm ngay vì có biến dạng dẻo.

Với thanh có độ mảnh < 105, sự mất ổn định xảy ra khi đã có biến dạng dẻo. Lúc này thanh bị oằn dưới một lực N không đổi, trên tiết diện thanh căng có vùng lồi và vùng lõm. Các thớ vùng lõm bị nén thêm, làm việc với Et=d/d (hình 3.14) - bằng hệ số góc của tiếp tuyến với đường cong biểu đồ kéo, nên Et còn gọi là môđun tiếp tuyến; các thớ vùng lồi bị giảm ứng suất, dùng E ban đầu =E.
Trên tiết diện đang xét, luôn tìm được trục z-z mà ứng suất không thay đổi ∆=0, gọi trục trung hòa – điểm O (hình 3.14b) (thường không trùng với trục trọng tâm tiết diện z0-z0), nằm bên thớ kéo tiết diện. Sự biến đổi của ứng suất trong mỗi phần sau khi có hiện tượng oằn:
∆1=Et.∆ (Phía tăng tải nén thêm do ứs uốn phụ thêm do thanh cong)
∆2=E.∆ (Phía giảm tải)
Trong đó ∆ là biến dạng uốn của một thớ bất kỳ, phụ thuộc vào y là khoảng cách thớ đến trục z. Có thể viết được ∆=y/

Hình 3.14. Trạng thái ứng suất-biến dạng thanh nén đúng tâm khi mất ổn định: a- biểu đồ ứng suất; b- tiết diện thanh

Năng lượng mômen ngoại lực gây bởi lực nén N khi thanh cong Me=N(+a) bằng năng lượng mômen nội lực Mi, xác định dựa vào tổng tích phân trên diện tích A1, A2 (hình 3.14,b):
 

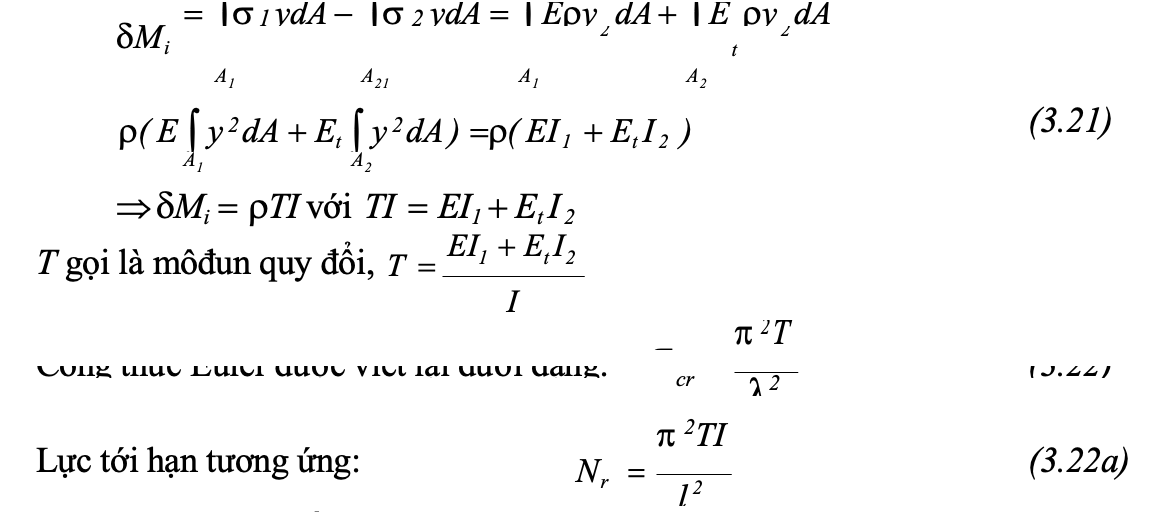
Ngày nay lý thuyết môđun tiếp tuyến được công nhận, dùng làm cơ sở cho việc lập các công thức tính toán trong quy phạm các nước. Tuy nhiên các công thức quy phạm của các nước không giống nhau là do xét đến các yếu tố khác nhau về vật liệu, về sai số chế tạo, v.v…
Trong thực tế, k ông thể có sự nén dọc trục hoàn toàn, mà luôn luôn có những nguyên nhân gây thêm sự uốn như độ lệch tâm ngẫu nhiên, độ cong ban đầu. Do đó, cấu kiện chịu nén dọc trục phải được tính toán như nén lệch tâm với độ lệch tâm ngẫu nhiên eef (do chế tạo, vận chuyển, dựng lắp, liên kết thanh vào nút ….).

Kiểm tra ổn định của thanh chịu nén xét thêm lệch tâm ngẫu nhiên ( cr,e) sẽ là:

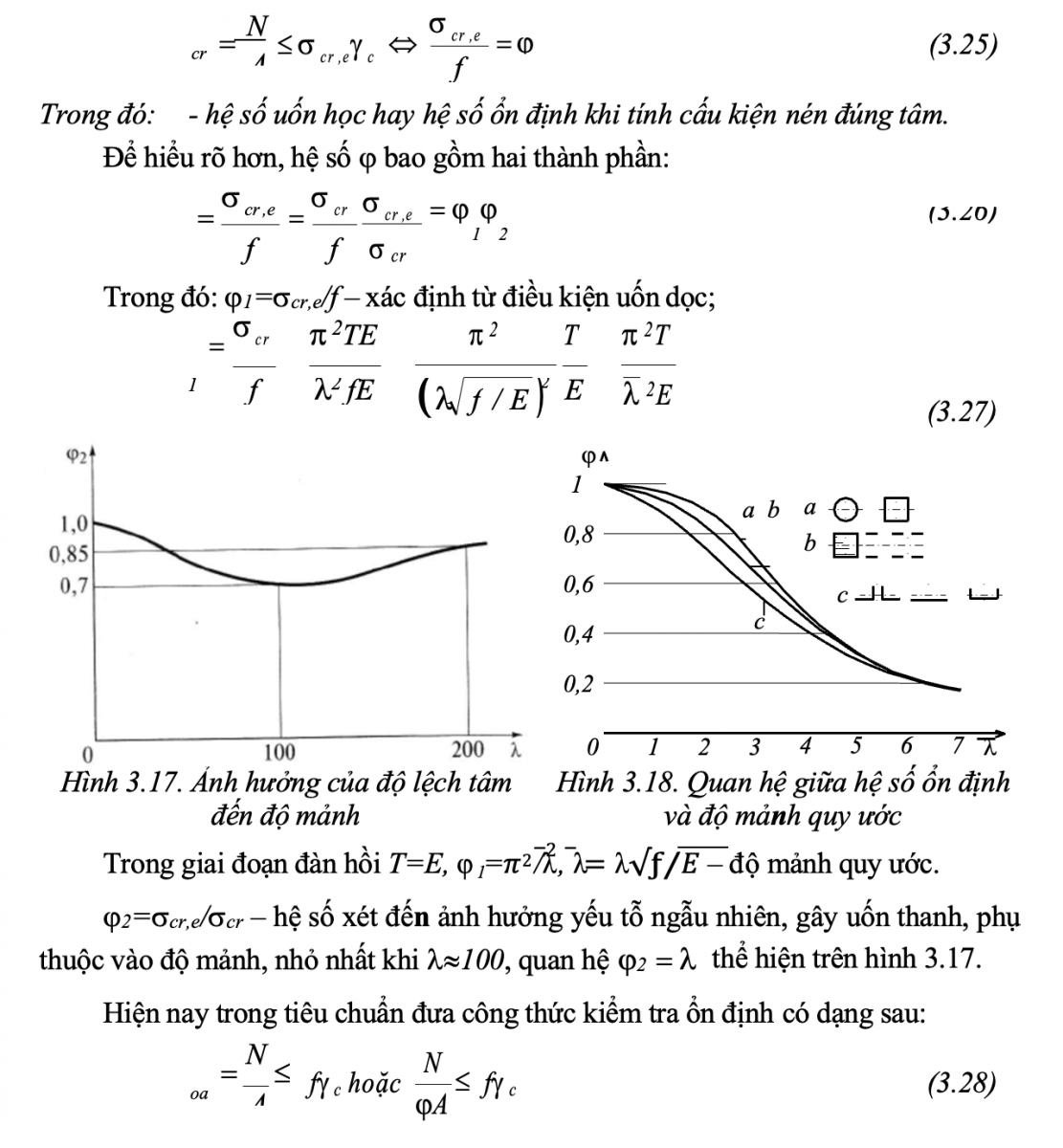
Trong đó: Hệ số  phụ thuộc vào độ mảnh của thanh và vào cường độ tính toán của thép, hình dáng tiết diện. Theo hình dáng tiết diện chia ra ba nhóm: a, b, c (hình 3.18). Quan hệ giữa  và ̅ theo hình dạng tiết diện được thể hiện trên hình 3.18. Trị số của  được cho trong bảng D.3 –PL theo độ mảnh  hoặc độ mảnh quy ước  (bảng 3.1). Khi tính toán trên máy tính, có thể xác định  bằng các công thức (6.7), (6.8), (6.9) - chương 6.

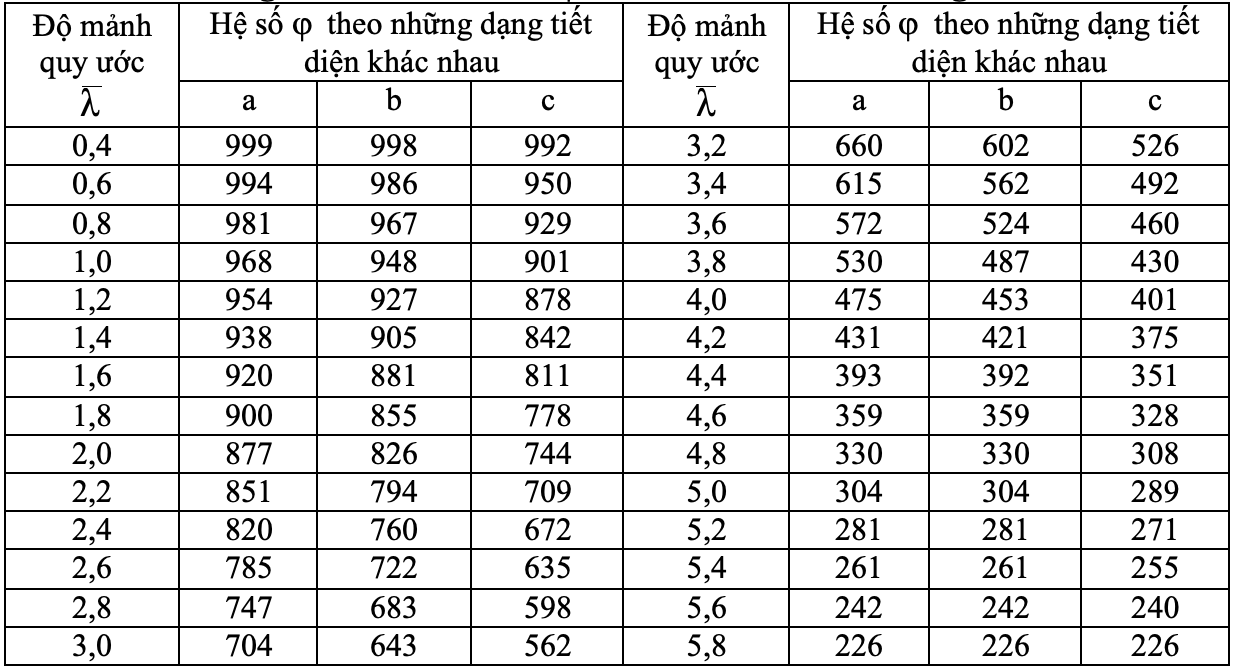
Bảng 3.1. Hệ số uốn dọc  của cấu kiện chịu nén đúng tâm

Chú ý: - Giá trị  trong bảng đã được tăng 1000 lần.
Hình dạng tiết diện a, b, c, độ mảnh quy ước giới hạn xem bảng 3.2.

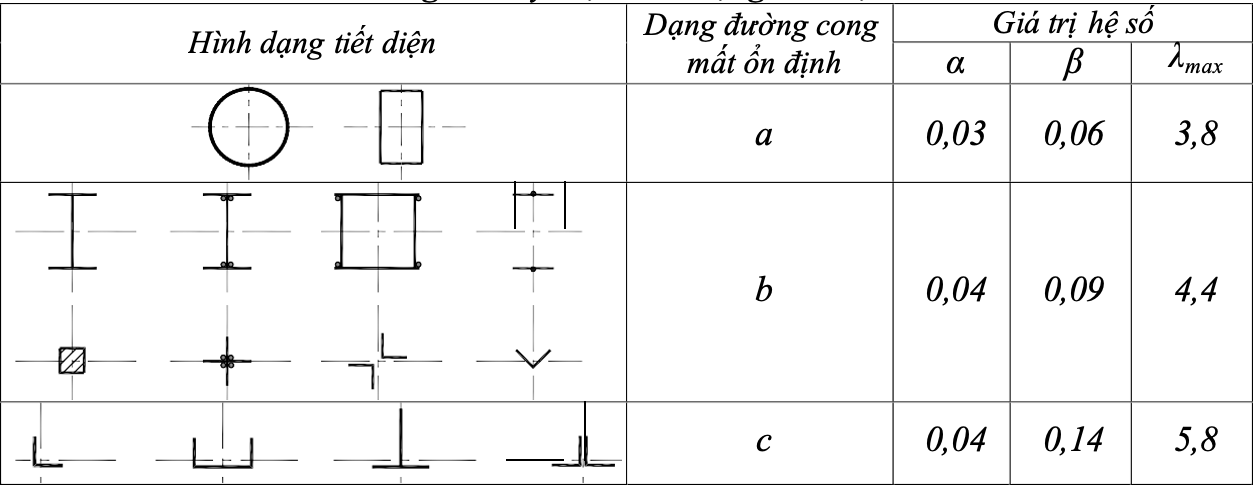
Bảng 3.2. Ký hiệu hình dạng tiết diện